霧島簡評113學測數學A
一年一度的學測數學又要來了!
連續三年110、111、112都有著高難度之稱的學測數學A
今年113年的學測數學又會怎樣呢?有沒有很興奮?
題目在這,有興趣的不妨自己寫寫看吧
前陣子忙了許久,沒在第一時間打好文章,不過這次要趕在過年前發文
也參考不同做法,供大家比對切磋。有錯都歡迎指出。本次有一些手寫來試試看,字醜抱歉了,(畢竟我懶…
以下就來看看吧,會針對每題做些講解,以及個人心得的部分。
(沒錯,就是要評價題目)
開始吧!
第壹部分:選擇題
一、單選題
(1)
我直接用手寫作圖來講解
注意a也是變數將x=0代入得到f(0)這個由a控制的三次函數
此時將其令為g(a)=f(0)得到一個g(a)的三次函數
由此便可討論g(a)>0的範圍,才可判斷有幾個a符合。
難度開始有了,明顯比前兩題難,有小創意。個人覺得屬於中間的題目。考驗抽象思考與多項式熟練度。
(2)
法一:
畫圖法 :一個是 sin 函數向上平移,一個是向左平移,都可畫圖會
引用和差化積公式: (有興趣可以看我以前的文章:為什麼要學「積化和差,和差化積」?
如果是手寫題要詳細寫過程的話,屬偏難,要詳細說明到底是2個交點還是3個交點,絕不能含糊帶過!
但考量是選擇題,難度會下降中間偏難,不少人應該會如果法一用作圖 加上帶點判斷。
依然是一題考驗細心程度的一題,考慮詳答的話會是可能會變單選最難的。
(4)
很有趣的排列組合題目,跳脫一般思維,要多想想,本身是不難的,
對於中間程度應該都可答對,再次驗證排列組合真的很活。
我覺得單選最有創意的好題目。知道中位數、組合數的概念即可作答,沒有什麼數字的計算,只有概念的想像!
考試中想不到 建議可以把數字設小一點,自己排看看會比較有感。
(3)
容我直接PO 手寫的過程 應該看得懂吧
法一:設坐標
法二:餘弦定理
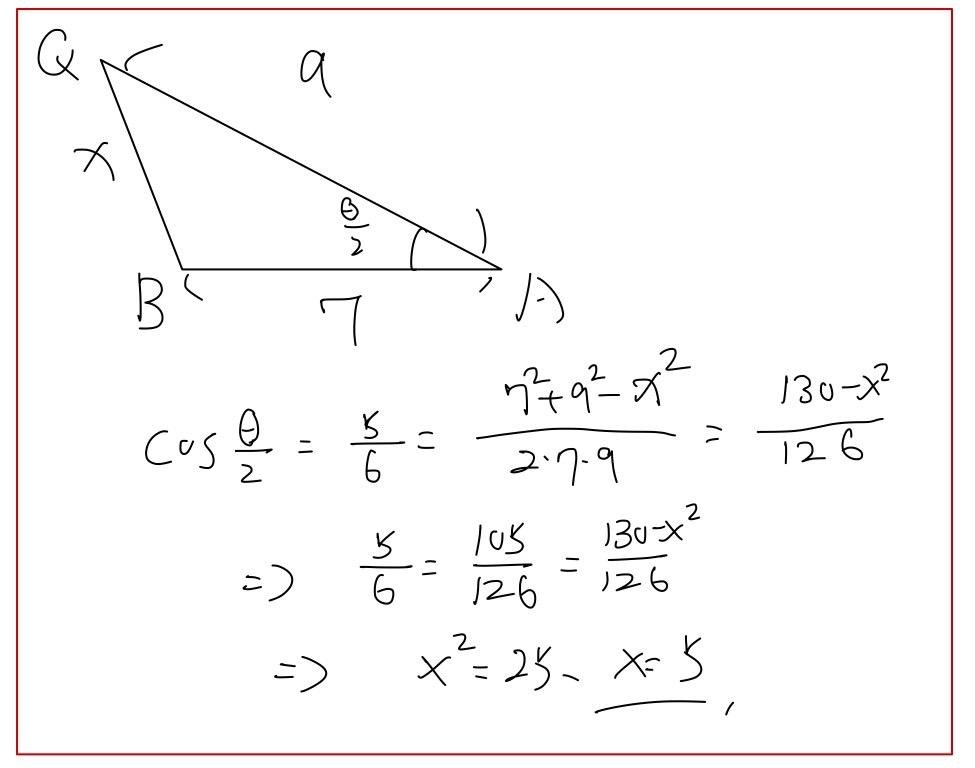
小無聊的計算題…很中規中矩。
難度算中間吧,考驗將應用問題轉化為數學式子,還有是否熟悉半角公式、設坐標等操作。
單選部分,1、2最簡單,(甚至是送分的程度),3、5、6中間,4最有難度。
且以5排列組合這題最有創意。
二、多選題

在此附上圖做解析。
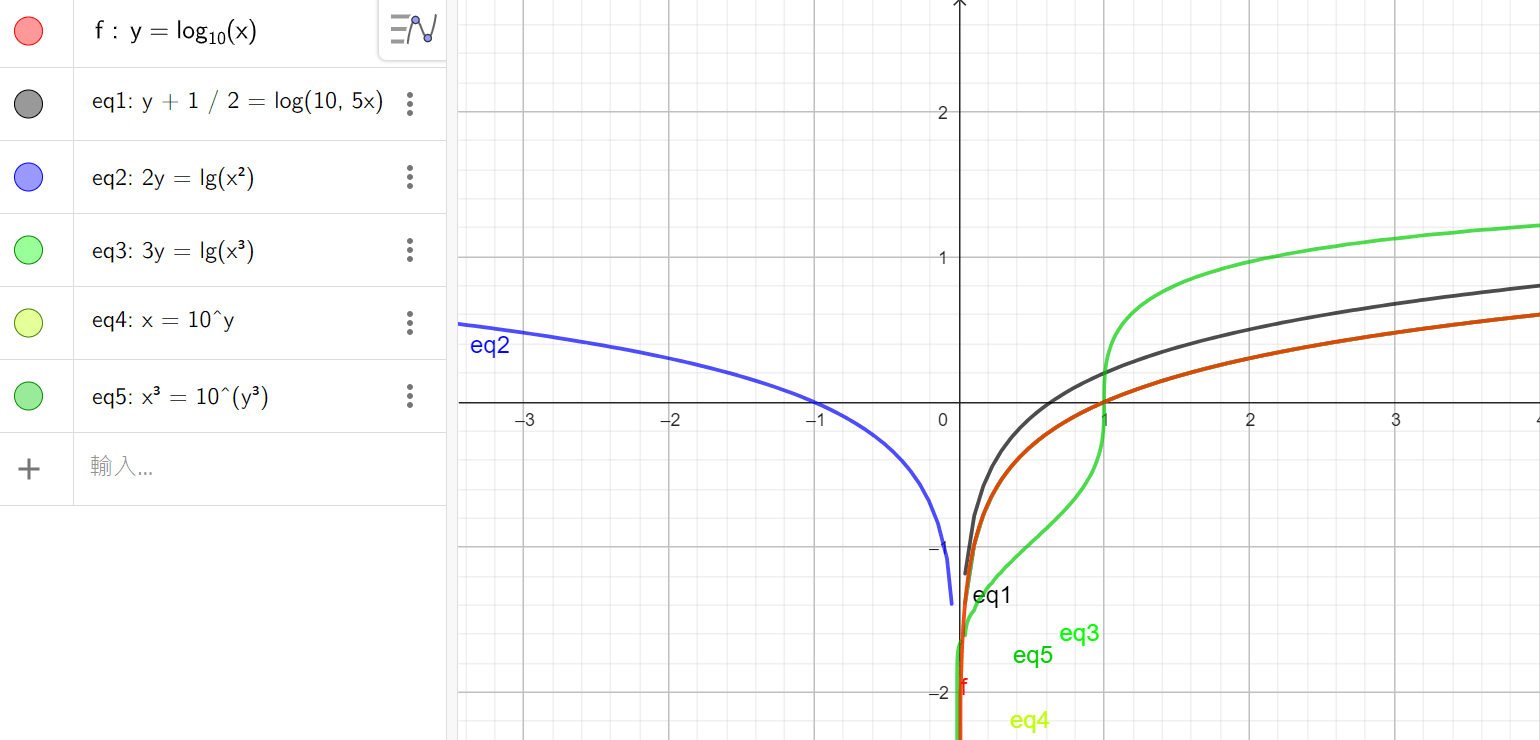
出得不錯的觀念題,不難,考的就是大家對於對數函數的概念、定義域與值域是否熟悉。
出得不錯的觀念題,不難,考的就是大家對於對數函數的概念、定義域與值域是否熟悉。
如果只會背對數律,那就慘囉。
(難一點的話,加上絕對值、三角函數、二三次多項式函數一起考 綜合觀念)


我想歸類於簡單。考很簡單的三角學知識,就算放在國中會考也還可以。還附上海龍公式,真是貼心啊,沒意外會是答對率最高的多選題。
但我覺得可以想一下:如果問題換成內切圓半徑、外接圓半徑、餘弦值等是否會有等差數列?等比數列?(對於任意的n)最大角是不是遞減?可自行調整問題作嘗試看看。
(當別人只完成1到10的項目,那麼想要超越他們就試著將1到20項全部完成,甚至是難度更高變化更多的10項、20項)
我覺得最無聊的一題。寫起來拖時間跟精力
考了迴歸直線、平均數、標準差的變換、點到點距離公式、點到直線的距離公式,以及更多的計算細節。
考量到計算量大,屬中間偏難,畢竟計算量大還是頗耗精神的
還是有什麼意想不到的妙解? 知道的歡迎提供。
(3)(5)
一樣用手寫如下
偏易,其實真的不難,敘述改一下,國中生也可以做,除了斜率跟向量是國中沒有的東西,其他都可以放在國中問了。
(2)(3)
將二元一次方程組與機率做結合,要考慮解的情況、另外要考慮機率的部分,最後還有條件機率,
整體歸類偏難。
(2)(4)(5)
考了矩陣的線性變換,跟三角概念,考點不少,算中偏難。
多選簡評:整體來說中間,跟去年前年比起來確實如此,多選題變簡單了。多選9特別麻煩…
三、選填題
簡單,同樣也是放在國中會考沒問題的一題 (雖然在國中會變成較難的題目)
坦白說蠻送分的。
a=-3 , b=3
不要看多項式好像很複雜,其實善用同餘的概念即可順利解題
難度歸類在中間好了,感覺很能夠鑑別強弱
程度的好人列式依然可以解出,程度差點大概會直接死去
25元
中規中矩的期望值題目,真的還好,中間偏易。應該大多數人都可以答對。
法一:幾何作法
最後一句是正射影長才對
法二:用向量去做
本卷的大難題,題意不難理解,問題是如何解出就是難處,而且應該很多人忘記正射影
估計答對率會在20以下,屬於難,但並非解不出來的類型。而且從題目的設計還是可以看出不少巧思的(如一開始兩向量垂直、直角三角形3,4,5) 數字設計得漂亮。
不妨想想看,如果一開始兩向量並非垂直的話,要怎麼辦?
其實也可以不用算區域III,IV的情況,因為沒意外就是對稱的
但保險起見還是列出來吧
我認為本卷真正意義上的大魔王題
敘述夠抽象,很純數學,無法像其他題順利列式解題,大多數人看到都會傻眼、無法理解題意。而就算理解題意,也不見得可以解出來。
將直線方程式、一元一次不等式考得非常之精妙。
另外,其實只看區域I,II的話,求出兩直線所交的點即是重心區域I,II的,紅色兩直線也就是中線。或許可以用其他幾何的觀點去做解題? 可以多想想看這是巧合嗎?
其實真的錯這題無可厚非,太有難度的題目直接跳過去做其他題才對。
不禁佩服出此題的老師很厲害。素養之高的厲害。太精彩了。估計答對率10上下,搞不好會有個位數的答對率,絕對能夠擠身於歷屆經典難題之中,
填充部分:就屬最後兩題16、17最為精彩,相信這兩題答對率應該都偏低才對,但其他13、14、15這三題真的就屬基本到中間的了。
第貳部分、混合題或非選擇題
此題單選 應該算蠻簡單的,空間向量 、 空間中的平面 這邊的基本題
此題就比較有挑戰性,要根據角度的範圍,在轉化成cos值的範圍
從而列出不等式,才可以推出題目所要求的不等式。
本身概念不難,但最後的計算數字確實要小心,雙重根號那邊可以先把4提出來就先提出來,相信這題也會讓不少人錯。混合後兩題有小難度,畢竟是要手寫證明的。
結論:
本次113學測數學A,到此結束,我認為難度是108課綱目前最簡單的,頭兩次的111、112都很難,至少這次基本題都有出來,難度上應該比較均勻一點,不過我看很多人還是預估五標跟去年一樣,我是期望應該要升高一些啦
本次最難題:選填17,絕對是大魔王,次難選填16,多選比較難應該是9、11、12
最佳思考題:單選5、單選4
好吧,其實本次有點小失望,算簡單的有5至6題 (單選1、2、多選8、10、選填13、15)換言之,這些基本分沒拿到就蠻不應該的。真正難的不多,難的可能是計算量大吧,相比前三年的「精彩」,這次感覺收斂一點。
仔細想想110、111、112這連續三年真的太精彩了,110是最後一次的99課綱學測數學,許多定理與觀念是他們發光發熱的最後舞台。111是首次的108課綱的學測數學A,要告訴世人,課綱弱化,不代表就能考簡單。112作微調,但還是展現了難度。
預估五標:12、10、7、5、4 (亂預估的
加油吧!每日都要學習數學!也必須欣賞數學之美,這份或許不像去年與前年那麼兇狠,但還是有精彩又難的題目,值得好好欣賞!
數學就是這麼美麗不是嗎?
最後感謝你的閱讀。
有什麼問題都歡迎指教。有什麼意見都說,有誤的地方請大聲斥責。還請多多關照。
現在是過年是吧
別說我掃興
何時何地都要讀數學
希望對社會大眾能有點幫助;想要數學更強的人、喜歡數學的人、學不好數學的人、對學校中的數學沒興趣的人、覺得數學沒用的人、覺得數學無聊的人... 都可看看。
數學是很有趣的。數學是很偉大的!數學就是純粹的美!
招待不周!