自然多數很神奇,但生活中不知道哪裡能應用?一般人無法體會e的神奇之處
本文算式圖片設計以深色模式為主,閱覽前建議切換為深色模式。由於手機 App 在切換樣式前需要強制重啟 App,若你是日間模式使用者,請在切換前利用「收藏」功能,避免切換完模式以後找不回本文。
凡事都是相對的。
我們知道,如果想要利用數學工具求得答案,時常要用到反向的運算來達成目的。比如說你現在 24 歲、你姊姊 27 歲,你想要知道你的年齡加上多少會等於姊姊的年齡,那你就要利用減法來得到 3(歲);比如說你的戶頭存款有 250 元、你的同學存款有 7500000 元,你想要知道你的存款乘上幾倍會等於他的存款,那你就要利用除法來得到 30000(倍)。
冪運算也同理,我們需要一個針對冪運算來反向運算的工具。這篇算是為了接下來要講的對數微分法鋪路,我們今天就來講講所謂的對數函數 log 吧。
。複習冪運算
冪(ㄇㄧˋ)運算就是我們平常講的「次方」,而乘上的次方數,被稱為指數。
從加減乘除來看,我們知道乘法就是連續的加法:
5 × 3 = 5+5+5
那麼冪運算就是連續的乘法了:
5³ = 5×5×5
我們還可以根據乘法擴展出指數的規律:
這些概念對於大部分的人來說都很熟悉,因為它就是個連續的乘法而已,當然我們也可以利用除法來推斷出:
一般來說我們知道如果一個正數不斷乘上某個大於 1 的數,那它增長的速度只會越來越快。
指數型增長有多可怕?假設現在培養皿裡面有一顆細胞,它每過 10 分鐘就會分裂一次,分裂出來的細胞還可以再繼續分裂下去。起初的 30 分鐘,1 顆變 2 顆、2 顆變 4 顆、4 顆變 8 顆,看起來還不算非常驚人,但經過了 5 個小時(30 次分裂),培養皿就從本來的 1 顆變成 10 億多顆細胞了!這種增長模式就是我們平常在說的「指數型成長」,寫成數學式子可以這樣表達:
反之,如果我們每天往一個裡頭已經有 2000 元的存錢筒投入 100 元,經過 30 天,裡面的錢也只不過是 5000 元而已——這樣每次增加一定量的增長模式就是「線性增長」,因為我們把它畫成函數圖形的時候會呈現一條直線。
。拆解冪次的工具:對數
就像剛才所說的:倘若現有一組線性的關係,因為它就只是一條單純的直線,我們通常可以用簡單的加減乘除來拆解它、預測它——但涉及冪次運算的指數關係就不同了。為了把指數關係變得像線性關係一樣單純,數學家定義了「對數函數」,把指數直接提出來:
log 10 = 1(因為 10 是 10 的 1 次方)
log 100 = 2(因為 100 是 10 的 2 次方)
log 1000 = 3(因為 1000 是 10 的 3 次方)
log 10000 = 4(因為 10000 是 10 的 4 次方)
……
千萬不要覺得它很可怕,它只是一個函數,只不過把函數的名字取作 log 罷了。當我們遇上了指數增長的關係,我們就可以利用 log 函數來簡化運算。
。對數的用法
不過這還不是全部。
我們回歸到 log 的本質:既然 log 函數是用來計算 10 相乘的次數,也就是把「10 的連續乘法」轉換為「1 的連續加法」,那麼裡面的數字相乘,對於 log 函數的值的影響也只不過是加起來而已:
log(1000×100) = log[(10×10×10)×(10×10)]
= log 1000 + log 100 = 5
簡單來說:
log(AB) = log A + log B
有了這樣的特性,我們就可以把原先難以計算的指數提到 log 函數外面,最後變成線性的關係,就能夠以單純的加減乘除來計算。
不過,如果今天我們要求取的對象不是 10 的整數次方呢?100 是兩個 10 的乘積,那麼 200 呢?
這裡就要用到 log 的規律來解決了,我們可以得到:
log(200) = log(10×10×2) = log(10) + log(10) + log(2) = 2 + log(2)
也就是說:200 是 10 的 (2 + log 2) 次方。這裡的 log 2 表示的值,意思就是「10 的『log 2』次方會等於 2」。
經過數學家的計算,log 2 大約等於 0.30102999566,通常取到 0.301 就很夠用。換句話說,10 的 0.301 次方,大約等於 2——至於數學家是怎麼從 2 算出 0.301 的?不要問,這很複雜,可能會講到天黑。
這樣的概念可能很抽象,不過有了這些規律,我們就可以簡化很多計算流程。
直接實作吧。假設你的存款現在有 20000 元,每年會有 1.1% 的利息,像這樣以複利模式計息,經過 n 年以後,你的存款應該會是 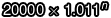 元。
元。
如果我們想要知道「不另外存錢進去的話,總存款何時會達到 22000 元」,那我們就可以根據問題列式:
接下來把式子整理過,兩邊同時除以 20000,右邊就變成了 1.1,接著再按照我們之前提到的等量公理:「在 A = B 的情況下,因為它們兩個本來就是相同大小的東西,所以必然有 log A = log B」:
就可以得到結果:「過了 9 年,你的總存款會達到(超越)22000 元。」
你會注意到,整個計算環節裡面最困難的地方就是求取 log 1.011 和 log 1.1 的值。一般來說在這算這類東西的時候,我們可以利用對數表(已經把常用 log 值計算好並且列出來的表)或者是直接從電腦利用計算機求取。
只要有了對數工具,像這樣的指數問題,就能直接把難以處理的指數提取出來成為係數,讓問題變得更簡單。即使今天本金的數量改成別的數字,我們仍然能夠循著同樣的模式快速地得出我們想要求取的東西。
不只這樣,我們日常中用到的聲音分貝單位、地震芮氏規模,它們的計算也用到了對數。地球上發生的不同地震能量差距可能非常大,所以科學家定義地震規模每相差 1.0,能量的釋放就相差「10 的 1.5 次方」倍(差不多是 32 倍):
log E = 4.8 + 1.5M(E 為能量,M 為地震規模)
所以,規模 5.0 的地震和規模 9.0 的地震,它們之間的能量就相差了 1,000,000 倍了。用這種方法來表示地震的能量就會很好懂,人類也才不會陷入像七龍珠一樣「每個怪物的戰鬥力都爆表,但因為位數太多所以感受不到誰強誰弱」的情況。
。更多種類的對數
雖然我們已經很習慣用十進位來衡量一個數的大小,但有些時候也不是非要用 10 當標準不可。log 其實也可以拿其他的數字作為標準,比如說我們把標準訂為 3,就有:
我們讀作「log 以 3 為底的 81,等於 4」。
這意思就是,81 是 3 的 4 次方,所以我們把它取以 3 為底的 log,就會得到 4。如果今天我們取 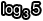 ,會得到 1.46497352072……換句話說,3 的 1.465 次方大約等於 5。
,會得到 1.46497352072……換句話說,3 的 1.465 次方大約等於 5。
一般來說這個寫在下面作為基準的小數字 a 稱為「底數」,被取的數字 b 稱為「真數」,不特別去指定底數的話就是 10。
。自然對數
在微積分的相關領域裡,就不愛使用以 10 為底的 log 對數了。
數學家們曾經證明:
這樣一個式子最後會收斂到一個無理數 2.71828...(還沒學過 lim 符號的話可以看看《數學的極限:友達以上,戀人未滿》),這個常數被稱為「尤拉數」,一般來說我們會用小寫 e 來表示。它具有一些奇怪的性質,例如:
也就是說,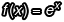 函數上每一點的值跟切線斜率正好都是
函數上每一點的值跟切線斜率正好都是 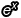 ,而這個特性也成了日後微積分學(特別是微分方程)裡被廣泛利用的工具。
,而這個特性也成了日後微積分學(特別是微分方程)裡被廣泛利用的工具。
以 e 為底的 log 函數,我們記作 ln(讀作 natural log,注意是小寫 L 而不是大寫 i),意即:
可以發覺到,其實生活中還是有很多東西需要用到對數觀念的,只是看你要不要去深究它而已。也許你買菜用不到 log,但你把工作賺來的錢存進銀行的時候,對數就成了很方便的計算工具。