達人專欄 本文算式圖片設計以深色模式為主，閱覽前建議切換為深色模式。由於手機 App 在切換樣式前需要強制重啟 App，若你是日間模式使用者，請在切換前利用「收藏」功能，避免切換完模式以後找不回本文。
在先前的文章曾經說過，數學工具都是一體兩面的：有加就有減、有乘就有除、有指數就會有對數。在微積分當中，微分也同理——有微分就會有積分。
說是這麼說，但「微分的逆運算是積分」這件事情其實並不是數學家事先就已經準備好的前提，而是經年累月發展出來的結論。要想瞭解積分的原理，我們就得先從函數圖形的面積開始說起。
。曲線下的面積，和微分有什麼關係？
為了方便計算，我們先舉一個簡單的函數吧！假設現在座標平面上有一個函數圖形：
y = f(x) = -0.5x² + 4
我們隨意取 x ∈ (1, 2) 的這一段來舉例：
根據我們從小到大學過的數學，要想直接取得塗色部分的面積，那可是不容易的。我們都知道，只要把矩形範圍的長寬相乘就能得到它的面積。然而，如果今天遇到的情況像上圖一樣不完美，那想必它不會像矩形一樣可以輕易解決。
對於這樣的問題，數學家的做法也用到了微分的原理——「尺度越細，估得越精準」。
我們試著把這個圖形沿著 x 軸切成 5 等分來看：
切成 5 等分後，塗色部分的面積和我們真正想求的面積仍然有些誤差。
改成 10 等分：
改成 20 等分：
我們可以從上面的做法得到這樣的結論：只要把想估計的圖形切成越多個長條，那麼這些長條的面積總和就會越接近這個圖形的面積，而當它趨近於無限等分的時候，長條面積的總和也會無限趨近於所求的圖形面積。有沒有覺得很熟悉？
先不要急著實證無限等分的情況。回到剛剛最初的 5 等分，我們把這 5 個矩形的長寬列出來：
可以看到：
左邊數來第 1 個矩形的高為 f(1)、寬為 0.2
第 2 個矩形的高為 f(1.2)、寬為 0.2
第 3 個矩形的高為 f(1.4)、寬為 0.2
第 4 個矩形的高為 f(1.6)、寬為 0.2
第 5 個矩形的高為 f(1.8)、寬為 0.2
得到 5 個長條的面積總和為：
A = f(1)×0.2 + f(1.2)×0.2 + f(1.4)×0.2 + f(1.6)×0.2 + f(1.8)×0.2
改成 10 等分的情況，就變成：
A = f(1)×0.1 + f(1.1)×0.1 + ... + f(1.9)×0.1
改成 20 等分的情況，就變成：
A = f(1)×0.05 + f(1.05)×0.05 + ... + f(1.95)×0.05
雖然透過這樣的做法得到的面積會隨著我們的等分數量提升而變得越來越精準沒錯，但單純只是這麼做的話沒辦法達到我們想要「無限趨近」的嚴格要求，而且要計算的項目也只會越來越多，勢必要找個方法可以完美簡化它。
。從微分到積分
注意到了嗎？我們一直在把每個等分矩形的寬度縮小，假設每個等分矩形的寬度都是 k，這個 k 如果能夠趨近於 0 是最好的，所以我們要想辦法生出一個 f(x)‧k，而且同時還要知道這個 f(x)‧k 是否和其他的函數存在某些關係。
回來看看當初我們學微分的的時候，「微分」是如何求出來的：
注意到這裡，我們回想一下：只要 Δx 不斷向 0 趨近，那麼這個函數的 
就會成為我們的最終產物 f '(x)。如果把等式的兩邊同時乘以 Δx，就可以得到：
就會成為我們的最終產物 f '(x)。如果把等式的兩邊同時乘以 Δx，就可以得到：
（Δx 越接近 0，誤差越小）
當 Δx 趨近到幾乎為 0 的時候（記為 dx），等式兩邊的誤差可以小到忽略不計。意即，如果有個函式 f(x) 的導函數是 f '(x)，那麼就會有：
剛才在切矩形的時候，我們希望每個矩形的寬度 k 可以越小越好（dx）。如果把上面等式左邊的 f '(x)‧dx 對應到我們本來的 f(x)‧k，我們可以知道，如果有某個函數 F(x) 微分後會得到 f(x)，那麼循著上面的規律，我們可以得到：
我們稱 F(x) 是 f(x) 的「原函數」或「反導函數」，當然也可以反過來說 f(x) 是 F(x) 的導函數，畢竟 f(x) 本來就是從 F(x) 微分而得的。
也就是說，我們透過「微分的定義」得到一個結論：「如果單個矩形的面積是 f(x)‧dx，只要 dx 夠小，這個 f(x)‧dx 也會無限趨近於 F(x+dx)-F(x)，使得兩者可以相互代換。」
不過單就把「一個」f(x)‧dx 擺出來是沒有意義的，因為這個矩形實在是太小了，面積趨近於 0。我們試著把這無限多個矩形加起來：
第 1 個矩形：f(1) dx
第 2 個矩形：f(1+dx) dx
第 3 個矩形：f(1+2dx) dx
第 4 個矩形：f(1+3dx) dx
……
最後一個矩形：f(2-dx) dx
先不要急著計算加總！剛才我們說了，因為「只要 dx 夠小，則 f(x)‧dx = F(x+dx)-F(x)」，所以我們可以把第一個矩形 f(1) 視為 F(1+dx)-F(1)，把第二個矩形 f(1+dx) 視為 F(1+2dx)-F(1+dx)……以此類推。
每個矩形都代換一下，換成剛才等式右邊的東西，事情就開始變得不一樣了：
第 1 個矩形：F(1+dx) - F(1)
第 2 個矩形：F(1+2dx) - F(1+dx)
第 3 個矩形：F(1+3dx) - F(1+2dx)
第 4 個矩形：F(1+4dx) - F(1+3dx)
……
最後一個矩形：F(2) - F(2-dx)
我們知道這無限多個超細的長條矩形的面積總和，就是我們想求的曲線下的面積。從前面幾項可以觀察到，如果我們把這些代換後的矩形加起來，每個矩形的第一項總是剛好可以和下一個矩形的第二項相抵，這無限多個矩形加起來以後，竟然變成了「F(2) - F(1)」這樣完美的結果。
像這樣從一個函數求取特定區間裡所有無窮小變化的總和，稱為「定積分」。以今天舉出的例子而言，在 x ∈ (1, 2) 這個範圍裡，這個函數底下的面積總和，可以記作：
我們可以稱它為「函數 -0.5x² + 4 在區間 (1, 2) 對 x 的定積分」。
。它們之間的關係如何？要怎麼計算？
我們透過剛才的推導知道了，在 x ∈ (1, 2) 這個範圍裡，f(x) 曲線底下的面積等於 F(2) - F(1)，再來我們得知道如何求出具體的 F(x)。只要好好整理一下：
就可以很清楚地看到它們之間的關係了。
我們回顧一下冪函數的微分公式：
老樣子，先不要急，F(x) 的事情我們等等再說。
只要解答「誰微分以後會變成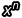 
？」這個問題，那我們就可以解決多項式的積分了。既然我們知道羃函數的微分是「先乘以目前的次方數，再把次方數減一」我們只要把羃函數的微分倒過來做就好了：「先把次方數加一，再除以目前的次方數」。
？」這個問題，那我們就可以解決多項式的積分了。既然我們知道羃函數的微分是「先乘以目前的次方數，再把次方數減一」我們只要把羃函數的微分倒過來做就好了：「先把次方數加一，再除以目前的次方數」。 一般來說只要多做幾次羃函數的積分運算，自然而然就會記起來了。記錯順序的話也沒關係，你可以把得到的原函數再微分回來，檢查看看是否相同，以作驗算。
像這樣求取原函數的過程，如果沒有指定積分的區間，稱為「不定積分」，記作：
（這條公式不考慮 n = -1 的情況）
也就是說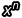， 積分以後會得到 
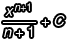，而 微分後會得到 。這裡你會注意到做完不定積分之後會有一個多出來的 C，這是為了應付所有可能。
積分以後會得到 ，而 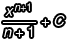微分後會得到 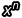。這裡你會注意到做完不定積分之後會有一個多出來的 C，這是為了應付所有可能。 什麼意思呢？我們假設今天有兩個函數：
y = x³ + 2x² + 3x + 2
y = x³ + 2x² + 3x + 7
這兩個函數對 x 微分以後得到的結果都是 3x² + 4x + 3——這個多出來的常數在函數圖形上的意義只不過是上下平移而已，對於函數的斜率一點都沒有影響——所以任何的常數對於 x 微分以後，結果都是 0。
也就是說，無論是：
y = x³ + 2x² + 3x
y = x³ + 2x² + 3x + 7
y = x³ + 2x² + 3x - √2
y = x³ + 2x² + 3x + e²
y = x³ + 2x² + 3x + π
這些函數微分以後，通通都會是 3x² + 4x + 3。既然如此，3x² + 4x + 3 對 x 積分就會有無限多種常數的可能性了，上面所列的這些通通都可以是 3x² + 4x + 3 的原函數，所以我們不如乾脆說它的原函數是 x³ + 2x² + 3x + C。
繞了這麼一大圈，我們終於可以把剛才最早舉的例子 -0.5x² + 4 拿去對 x 積分了：
透過不定積分得到原函數 F(x) 之後，定積分對我們來說就只剩下單純的代入計算：
由於在計算 F(b) - F(a) 的時候，待定常數 C 會在前後相減的過程中被抵銷掉，所以當我們想求取定積分，這個 C 就會自然消失，所以計算定積分的時候千萬不要自作聰明加上一個多餘的 C 上去，否則你的分數就沒了。
計算定積分的時候也要注意：函數值如果是負的，那麼積出來的面積也會是負的。假如想計算定積分的區間同時橫跨了正面積和負面積，它們之間就會互相抵銷：
所以在積分之前，必須先弄懂函數在哪些區間大於 0、在哪些區間小於 0，接著再分開來積分、把其中負的結果轉正，這樣才能得到正確的總面積。
。生活中的微積分
很多人學微積分的時候都會懷疑：「我學這個到底幹嘛？」
其實單就「微分」和「積分」這兩件事情來看，它們對於生活確實沒有什麼直接的影響，不過對於科學的發展，微積分就非常重要。如果你現在正在邊聽音樂邊看這篇文，那我也可以趁現在告訴你，你的電腦和手機播放音樂的時候也用到了微積分的觀念。
我們都知道，平常我們接收到、發出來的各種聲波，可以用類比訊號的形式畫成曲線圖形。然而在電腦的世界裡，說 1 就是 1、說 0 就是 0，類比訊號真要拿到電腦上面來的話實在是難以直接處理。因此，電腦便是用了像積分一樣的觀念，把聲波曲線切成很多個等分，切得越細就越精準（而不失真），我們平時聽到的「取樣率」就決定了聲波要被切成幾等分。
人類從最早的加法、減法逐漸建構出現在的數學，但微積分並不是數學的頂點。相反地，對於其他更深更廣的領域裡，微積分反而只是一個用來計算的基本工具而已，就好像我們使用加減乘除一樣。
平常在電腦上用到的 JPG 圖檔壓縮技術，也是基於從微積分發展出來的傅立葉轉換，你才得以用小小的空間儲存這麼多圖片（做個小實驗：隨便把你電腦裡的一張圖片打開，用小畫家另外存成 BMP 格式，看看你的圖檔大小會變得多恐怖）。
如果沒有微積分，現在的你說不定沒辦法像現在這樣天天上 Instagram 看大奶。
。碎碎唸
坦白講，要從原理層面弄懂「定積分」這件事情真的不簡單。在網路上搜尋「定積分」，大部分的文章只會說，微積分基本定理告訴你：
接著就是搬出一連串的題目要你算，也沒好好解釋這樣的結論到底怎麼來的，搞得你根本不知道積分可以幹什麼，就算知道了積分可以計算面積，也搞不懂為什麼「積分」和「面積」會扯上關係，即使回頭翻閱課本的嚴格定義，看來也像是天書。
記得在高中一年級的時候，因為一直想不通「為什麼定積分可以求得面積」這樣的問題，下課時間跑去盧了數學老師（兼班導）很久。後來她請了產假，就換成代課老師被我盧，直到那代課老師很細心地畫圖跟我解釋完前後項抵銷的問題，我的疑惑才終於解開。
所以我的大學微積分根本就是兩個高中的數學老師教的。
大概也是因為親身經歷過這種讓人很頭痛的瓶頸，才會在數年之後下定決心好好寫這麼一系列的微積分相關文章吧。也許這些文的推論過程不算嚴謹，但比起現在的大學生為了準備期末考而盯著考古題和原文書頭痛老半天，我仍然認為「先求懂再求好」才是最重要的。
如果有任何一個人因為我小屋的文章而受益，那我在電腦前熬夜寫這些也就都值得了。
