達人專欄 本文算式圖片設計以深色模式為主，閱覽前建議切換為深色模式。由於手機 App 在切換樣式前需要強制重啟 App，若你是日間模式使用者，請在切換前利用「收藏」功能，避免切換完模式以後找不回本文。
積分技巧可以粗略地分為三種：代換積分法、分部積分法、部分分式積分法。上禮拜我們講完了其中最基本的代換積分法，今天來講講分部積分法吧。
只要你會了微分乘法律，那你就已經先掌握了八成的分部積分法了。其實分部積分法的核心概念也很簡單：「只要想要積分的對象剛好是微分乘法律的其中一項，而且另外一項剛好也可以積分的話，那就可以試圖湊出答案來了。」
。微分乘法律和分部積分法的關係
直接從範例做起的話聽來一定會很抽象，我們就先從原理講起吧。
如果你還沒有把微分乘法律忘光的話，你會知道對於一個兩樣東西相乘而得的項 fg，如果要將 fg 對 x 微分，會有：
如果我們把等號的左右兩邊再同時對 x 積分一次（等量公理允許我們這麼做），左半邊當然就會被還原為 fg 了（畢竟微分以後又積分），右邊則變成一個看起來複雜的積分式：
但是不用怕，既然微分加法律（減法律）告訴我們，「先相加再微分」和「先微分再相加」的結果是相等的，那麼積分也同樣適用：「先相加再積分」和「先積分再相加」的結果也應該要是相等的。我們把等式左半邊的 dx 消除，同時把等式右半邊拆成兩個積分式：
然後簡化等式左半邊（其實左半邊可以寫成 ∫ 1 d(fg)，只是把 1 省略了），同時把右半邊可以相消的 dx 消除：
這就是分部積分法的公式由來了。不過一般教科書上習慣用 u 和 v 作為代換用的變數，移項一下：
。實際做做看
就拿上次所說的「只用代換法也無法解決的積分式」來當範例吧。如果有個積分式：
回顧剛才講的分部積分法的式子，對應一下，如果要套用分部積分法的話，我們必須：
接著好好想想每一項應該如何安排。
分部積分法裡面「uv」這項顯然不是問題，因為它不需要用到任何的積分，在代換過之後只需要無腦地把 u 和 v 相乘就可以得到了，所以這個 uv 先擺在一旁不用管也沒關係。
接下來最重要的問題在 u 和 dv：我們應該令誰為 u？令誰為 dv？
思考一下，這個積分式裡面有三個項：x、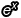
、dx。既然 dv 牽涉到「微小變動量」這檔事，那麼它一定會跟 dx 有關聯（因為 dx、dv 這種特殊的變數是透過微分才有可能得到的東西），所以這個 dv 要嘛應該設為 xdx，要嘛應該設為 
，然後剩下的設為 u，這樣才能夠讓 udv 等於原式的 
。
、dx。既然 dv 牽涉到「微小變動量」這檔事，那麼它一定會跟 dx 有關聯（因為 dx、dv 這種特殊的變數是透過微分才有可能得到的東西），所以這個 dv 要嘛應該設為 xdx，要嘛應該設為 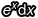，然後剩下的設為 u，這樣才能夠讓 udv 等於原式的 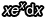。 根據上面這些判斷，它會有兩種可能性，第一種可能就是：
第二行的 du 跟 v 是由第一行推出來的，要分解動作的話就是：
在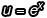 
的情況下，因為 
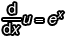，所以等式兩邊同乘以 dx 得到 
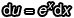；在 dv = xdx 的情況下，等式兩邊同時積分，得到 
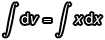，也就有 
了。
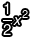的情況下，因為 ，所以等式兩邊同乘以 dx 得到 ；在 dv = xdx 的情況下，等式兩邊同時積分，得到 ，也就有 了。 先不要管第二種可能性是什麼，我們來嘗試第一種可能吧。既然都已經得到 u、du、v、dv，那麼依照分部積分法，只要把每一項對應上去：
Oops。情況似乎變得越來越複雜了，所以我們得到了「第一種可能性行不通」的結論，因為這麼繼續下去只會變得越來越複雜，永遠積不出結果來。
既然第一種可能失敗了，那來試試第二種可能：
剛剛的分解動作，它的觀念簡單來說就是：「如果要從 u 得到 du，那我們只要把 u 微分，然後再移項一下就會有結果；反之如果要從 dv 得到 v，我們只要把 dv 積分一次就可以還原出來了」。
照著分部積分法繼續做下去：
我們驚奇地發現，拼湊出來的 ∫ vdu 這一部分是可以直接積分的。繼續做下去，我們得到最後的結論如下：
不要因為太過興奮而忘記加上待定常數 C 了。
。LIATE 法則
從上面整個過程看來，我們可以感受到開頭「應該令 u 為誰、令 dv 為誰」的這步操作，關係到我們最後能不能積出這個式子。如果使用了前面提到的第一種可能性，那積分出來的結果只會越來越複雜，因為我們嘗試的路徑沒有剛好讓另一邊的 ∫ vdu 剛好能夠積出結果來。
問題來了：考試時間總是有限的。如果我們想要少走一點冤枉路，那麼在這些可能性當中，到底有沒有辦法預先判斷「哪一條路才是對的」呢？
答案是：有，我們有「LIATE」的順序，可以判斷應該優先令 u 為誰：
L（Logarithm）對數函數，比如：log x、ln x
I（Inverse trigonometric）反三角函數，比如：arctan x、arcsin x
A（Algebraic）代數函數，比如：x³、5x²
T（Trigonometric）三角函數，比如：sin x
E（Exponential）指數函數，比如：、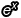
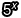
、 以剛才的例子，我們發現原式有 x 和 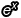，既然 x 屬於代數函數的一種，優先順序比 所屬的指數函數還要高，那我們就令 u 為 x、剩下的 為 dv，結果就是我們要的。
，既然 x 屬於代數函數的一種，優先順序比 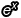所屬的指數函數還要高，那我們就令 u 為 x、剩下的 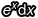為 dv，結果就是我們要的。 然而，它只是一個經驗法則，畢竟這個法則的順序是基於「通常怎麼樣的函數會比較好積」而總結出來的，某些時候它仍然有例外，所以參考看看就好了。
分部積分法就是這樣，因為只是照著微分乘法律而做，所以基本的概念理解起來並不難，但是題目一旦刁鑽起來，真的就會複雜得要人命。
有了分部積分法這樣的工具，我們就能積出更多種類的積分了。
