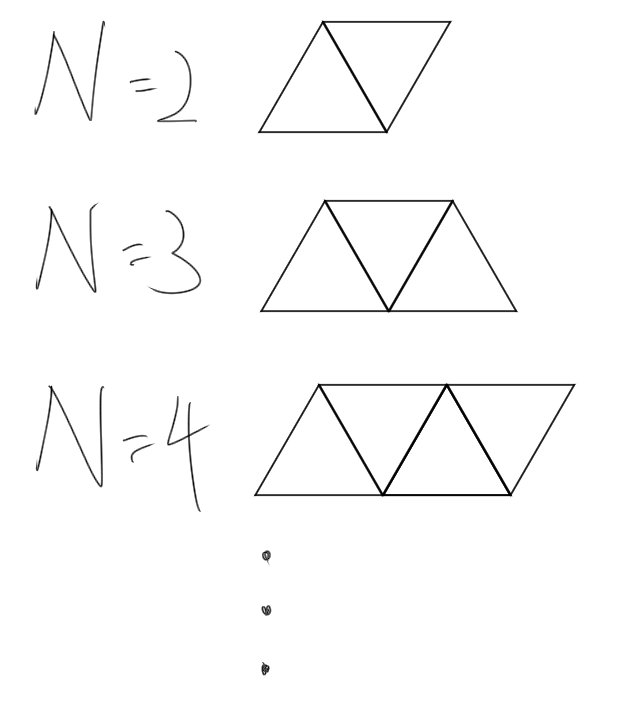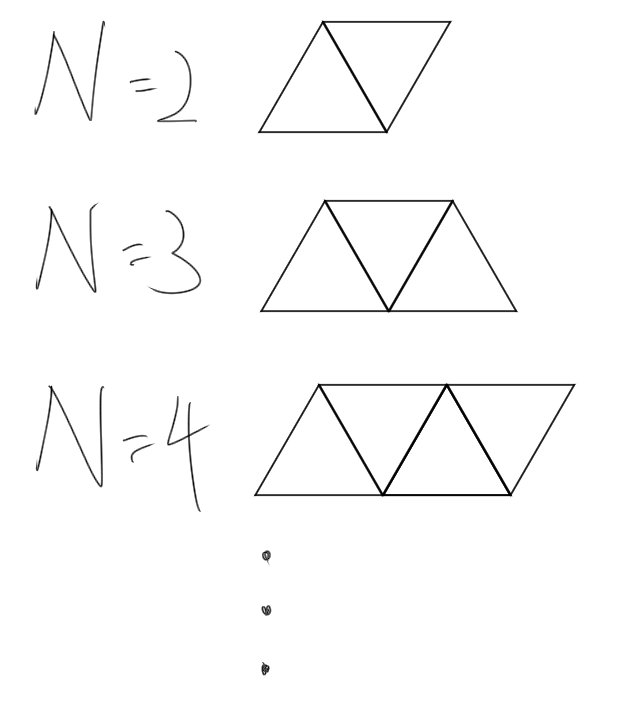題目連結:
題目大意:
輸入第一列給定一正整數 T(1 ≦ T ≦ 10),代表測試資料筆數,每筆佔一列。每列給定兩正整數 N 、 K(2 ≦ N ≦ 10 ^ 4、3 ≦ K ≦ 100),代表現在你有 N 個大小相等的正三角形,試問你是否可以藉由這 N 個正三角形拼湊出一個凸 K 邊形(三角形必須全部使用)。
其中正三角形的拼湊有以下兩條限制:
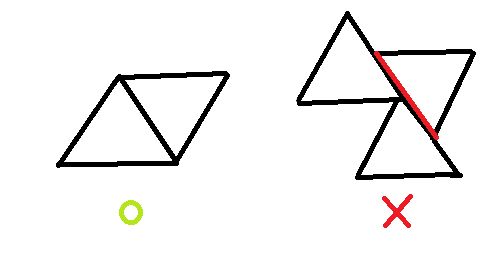
一,每個三角形至少要有一邊與其他三角形相接(N = 1,視為規則成立。即所有三角形應聚在一塊,而沒有獨立自己一區者)
二,兩個三角形之間的相接需為一邊「完整地」與另一邊重合。
如上圖中的左側即符合規則一、二;而右側則不符合規則二(且該圖形非凸多邊形)。
範例輸入:
5
2 3
2 4
4 5
6 6
7 7
範例輸出:
no
yes
no
yes
no
解題思維:
由於我們的目標是凸多邊形,因此其內角應皆小於 180 度。可以看到一個正三角形是 60 度、兩個正三角形拼在一起為 120 度,所以我們可以形成 60 度以及 120 度這兩種內角角度。然而這就是極限了,因為再多就剛好 180 度了,因此三個以上(含)正三角形形成一個內角是不可能的事情。
那麼根據上面的條件,我們實際上有機會可以湊出哪些多邊形呢?答案是 3 ≦ K ≦ 6 的這些傢伙們(3 ≦ K 這個條件很自然,畢竟至少三條邊才能圍成一個封閉圖形)。原因很簡單:
由於任意一個凸多邊形的外角總和為 360 度(簡單證明:讀者可以隨便拿個凸多邊形從任意一頂點開始繞一圈回到原點,過程中每次轉彎之角度即為一外角。而繞一圈後即回到原點並「面朝同方向」,因此外角總和為 360 度),因此如果存在外角太小則會使某個內角過大。而可以看到我們最大的內角為 120 度,因此外角最小只能是 60 度,不能再小。
因此可以看到
360 ÷ 3 = 120
360 ÷ 4 = 90
360 ÷ 5 = 72
360 ÷ 6 = 60
360 ÷ 7 < 60
……
因此當 K = 7 以上(含)時,其外角將必有一者是小於 60 度的。因此我們不可能湊出 K = 7 以上(含)的凸 K 邊形。
那在哪些條件下我們可以湊出 K = 3 、 4 、 5 、 6 呢?
(以下假設我們使用的三角形之邊長為 1,而這等等會派上用場)
首先是簡單的 K = 3 和 4:
當 K = 3 時,可以看到這個 3 邊形必須為正三角形(因為內角都是 60 度)。因此設其邊長為 s(因為一個單位正三角形的邊長為 1,因此 s 為正整數)。而正三角形面積之公式為
(邊長 ^ 2) × (√3) ÷ 4
因此比較一下這個組出來的大正三角形與組成單位之小正三小形之面積,可以得到我們需要 s ^ 2 個小的正三角形來組出大的。
也就是說當 N = 1 ^ 2 、 2 ^ 2 、 3 ^ 2 、 4 ^ 2 、……,即 N 為完全平方數時,我們可以造出一個 3 邊形。
接著是當 K = 4 時,可以看到 N = 1 是一個正三角形不是 4 邊形。但是除此之外的 N 值,我們可以按照下圖的方式
來形成 4 邊形。因此對於 N ≧ 2,我們都有辦法可以組成一個 4 邊形。
接著是 K = 5:
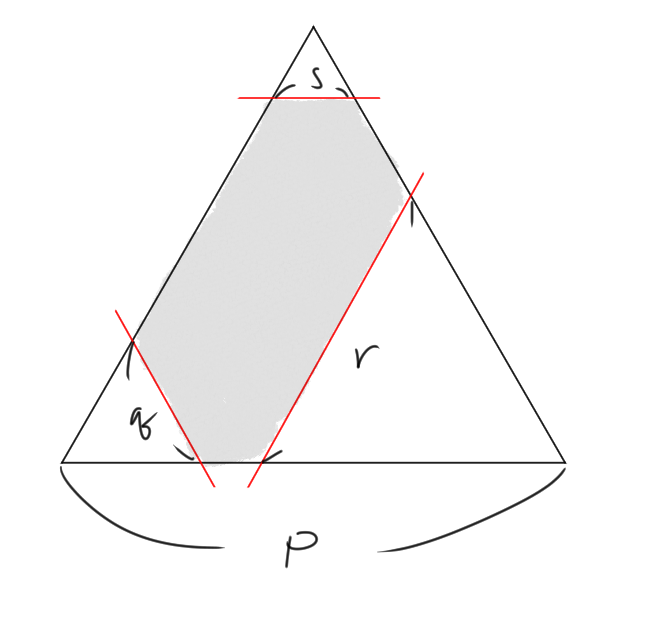
從內角的觀點出發,我們唯一可能的拼法是令其中一個內角為 60 度,其他四個則為 120 度,且 5 邊形的邊長為整數(因為單位正三角形的邊長為 1)。因此我們可以畫出下圖的 5 邊形(如塗成灰色之區域所示)
其中 60 度的角之兩腰與那個角的對邊,這三條邊往兩側延長可以形成邊長為 q 與邊長 r 的兩個正三角形(如上圖所示)。因此我們可以將這整個 5 邊形看成是一個較大的、邊長為 p 的正三角形,經由紅色的兩條直線切割掉邊長 q 以及邊長 r 的正三角形所留下的「面積」。
因此回到 K = 3 時的論點,邊長 x 代表其需要 x ^ 2 小正三角形所組成。因此我們可以看到這個 5 邊形實際上是由 p ^ 2 - q ^ 2 - r ^ 2 個小正三角形所組成。其中,可以看到 p 、 q 、 r 皆為正且因為 60 度的角之對邊的邊長應為正數,因此大的正三角形之邊長 p 應大於 q + r。
總結:當 X = p ^ 2 - q ^ 2 - r ^ 2 時(其中 p 、 q 、 r ≧ 1 且 p > q + r),我們可以用 X 個正三角形組出一個 5 邊形(只要按照上圖的方式排列即可)。
最後是 K = 6,而這其實跟 K = 5 的情況很像,如下圖
因此可以推得當 X = p ^ 2 - q ^ 2 - r ^ 2 - s ^ 2 時(其中 p 、 q 、 r 、 s ≧ 1 且 p > q + r 且 p > q + s 且 p > r + s),我們便可以使用 X 個正三角形組出一個 6 邊形。
接著的問題是,我們要怎麼判斷 N 個正三角形可以形成一個 K 邊形?K = 3 、 4 的情況比較簡單,不管是建表還是直接判斷都相當直接;而 K = 5 、 6,如果我們要直接判斷的話需要分解 N 這個數字(例如說 K = 5,則我們需要找到數組 (p, q, r) 滿足 p ^ 2 - q ^ 2 - r ^ 2 = N)。
但是對於 K = 5 、 6,說實話我沒有好的分解法或是窮舉法QQ。我在下方附的範例程式的應該是假解,窮舉 p 的範圍似乎沒有完全覆蓋到該有的。不過我也無法說明,希望有大大可以指點迷津。
本題實際上有一篇相關的論文存在,即
Eike Hertel, Christian Richter: Tiling Convex Polygons with Congruent Equilateral Triangles (2014)
裡面就是在討論本題之題目。而且還證明了 T5 的補集(T5 即為「可以湊出五邊形的正三角形個數」形成之集合,其補集即為除此之外的正整數)為歐拉(Leonhard Euler)提出之 Idoneal Number 這個有限數列的一個子集。而因為 Idoneal Number 本身的性質之緣故,因此與廣義黎曼猜想(Generalized Riemann Hypothesis)產生了連結。
而 T5 和 T6 的補集都是有限集合,因此其實也可以直接偷吃步窮舉補集的判斷即可。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。