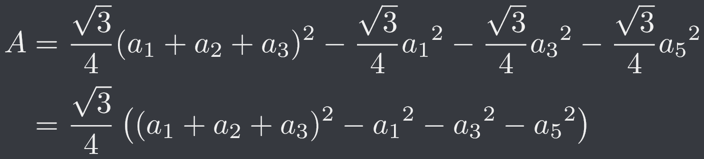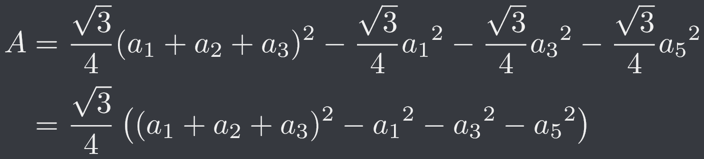題目連結:
題目大意:
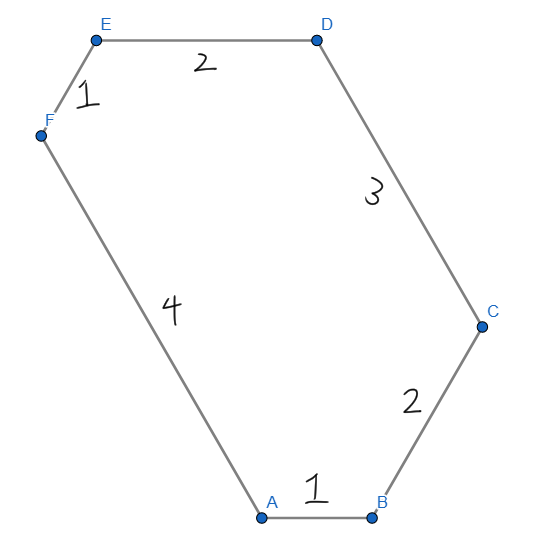
已知六個角都是 120 度且邊長為整數之六邊形可以被若干個邊長為 1 之正三角形所填滿。
輸入有多筆測試資料,每筆佔一列。每列給定六正整數 a1 、 a2 、 a3 、 a4 、 a5 、 a6(皆介於 1 ~ 1000 之間),代表以順時針順序給定一個內角皆是 120 度的六邊形之邊長。試問該六邊形需要多少個邊長為 1 的正三角形才能填滿?
範例輸入:
1 1 1 1 1 1
1 2 1 2 1 2
範例輸出:
6
13
解題思維:
既然題目已經保證了我們可以利用正三角形填滿給定的六邊形。那麼我們只需要算出六邊形的面積 A,除以單一一個邊長為 1 正三角形的面積,便可知道需要多少正三角形。
可以看到題目的六邊形可能會長得很畸形,如下面這個六邊形:
而再仔細觀察如上的六邊形,可以發現我們延長 BC 、 DE 、 AF 這三個邊(延長 AB 、 CD 、 EF 也可以)可以得到一個較大的正三角形,如下圖
(這邊我們將原邊長替換成題目的未知數,代表其他情況也適用)
而上圖中三角形 GHI 會是一個正三角形是因為:六邊形的所有內角都是 120 度,因此所有外角都是 60 度。使得 GHI 、HIG 、 IGH 這三個角也都是 60 度,也就造成三角形 GHI 將必定是正三角形。且我們可以看到其邊長為 a1 + a2 + a3。
於是我們便可以得到原先六邊形的面積 A 為
(正三角形 GHI 面積)-(正三角形 ABH 面積)-(正三角形 CDG 面積)-(正三角形 EFI 面積)
即
而單一一個邊長為 1 的正三角形之面積為
因此所求數量為
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。