題目連結：
題目大意：
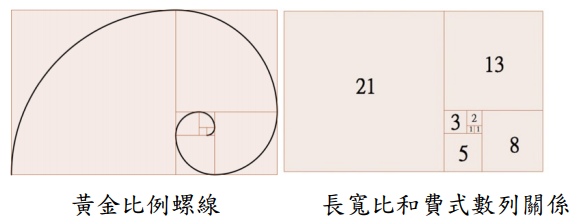
給定一正整數 n （1 ≦ n ≦ 45），代表用了前 n 項費氏數列之值作為 n 個正方形邊長，並排成一個長方形。如下圖為 n ＝ 8 所形成的長方形：
可以看到該長方形之短邊與長邊之比為 21:34 。
求使用前 n 項費氏數列作為正方形邊長所形成的長方形之短邊比長邊之值為何？
範例輸入：
範例輸入一：
6
範例輸入二：
8
範例輸出：
範例輸出一：
8:13
範例輸出二：
21:34
解題思維：
可以看到長方形之短邊為第 n 項的費氏數列。而長邊為第 n 項與第 n - 1 項之和，根據費氏數列的定義，其值為第 n + 1 項之數列值。
因為 n 不大，所以就直接求出第 n 項費氏數列與第 n + 1 項的費氏數列，所求即是兩者之比。而且不會超過 int 可儲存的範圍。
此次分享到此為止，如有任何更加簡潔的想法或是有說明不清楚之地方，也煩請各位大大撥冗討論。
