【劍靈】【數據分析】暴擊傷害率是怎樣算的？屬性數值關係曲線算式大拆解！

正文

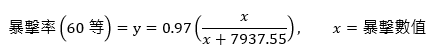
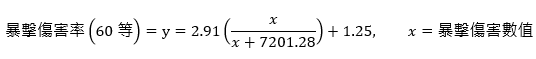
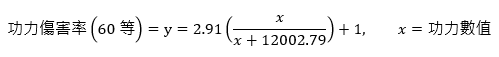
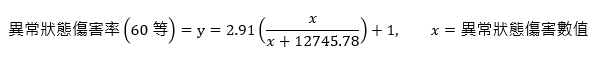
為甚麼要知道屬性數值跟率之間的關係？

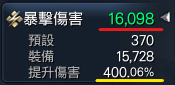
首先我們需要知道何謂屬性的「數值」跟「率」。以下兩張圖展示了無論是在面板上還是裝備描述上的暴擊傷害（下通稱「暴傷」）都有分為「數值」（紅色底線標示）和「率」（黃色底線標示）。

「圖1」個人資訊面板的暴擊傷害數值與暴擊傷害率

「圖2」神穹項鍊的暴擊傷害數值與暴擊傷害率

然而要怎樣得知一件裝備的效益呢？若要解決這個問題，那必定要先知道劍靈裡面的傷害計算方法。我們不妨從簡化版的傷害計算算式開始看（我同時亦有詳細研究傷害計算算式，若有機會，將會在另一篇文章分享）。

「算式１」傷害計算算式（簡化版）

從算式中可以看出，假設有暴擊的話，暴傷率的增幅將與技能傷害的增幅相等，也就是說暴傷率是可以直接套用在傷害計算上的。那現在我們就只需要考慮暴傷數值了。從個人資訊面板上可以得知，暴傷的數值跟率是呈正比關係的（也就是說，數值越高，率越高）。我們希望能找到一個函數(Function)能夠表達數值與率之間的關係。

對經濟學有基礎認識的朋友，應該知道一個經濟學的基本概念「邊際效用遞減法則(Law of diminishing marginal utility)」，指的是投入同一單位的資源越多，其邊際效用（所提升的效用）會越來越少的現象。劍靈裡面部份屬性的特徵同樣如此，數值越高，（在同樣的數值提升下）率的提升越少。舉個例子，當你暴傷數值為5000時，提升500暴傷數值會提升6.76%暴傷率；而當你暴傷數值為15000時，提升500暴傷數值則只會提升2.08%暴傷率（來自60等版本真實數據）。

擁有上述特徵的屬性包括，但不限於：

1. 暴擊
2. 暴擊傷害
3. 功力
4. 狀態異常傷害

下文將針對這4種屬性各自的關係函數進行分析。

---

如何找出各屬性的關係曲線算式？

沒有任何數據就不可能找出算式，所以我們先從收集原始數據開始。先假設遊戲內角色資訊面板上顯示的數字的正確的，透過不同裝備的搭配就可以得到不同數值下的率了。然後收集了以下數據：

暴擊（60級）	共54組，數值由0至19564
暴擊傷害（60級）	共80組，數值由0至16152
功力（60級）	共57組，數值由0至10422
狀態異常傷害（60級）	共23組，數值由0至6758

值得注意的是，有部份屬性在角色資訊面板上會受到其他因素影響，例如（龍銀會員的5%暴擊率、10%暴傷率／八卦牌五件套的暴傷率／幻神系列武器的暴擊率、暴傷率等），因此收集數據時需要按照該些項目進行調整。

第二步就是要把原始數據變成一條表達算式。如果我們把每一組收集到的數據放到一個以x軸為數值，y軸為率的坐標系(Coordinate system)上，再把數據點連起來的話應該會形成一條線，我們的目標就是要找出表達那條線的算式。這個過程剛好就是機器學習(Machine learning)領域中，其中一種常見的任務：迴歸分析(Regression analysis)。迴歸分析的目的在於了解多個變數間的關聯性，並建立一個模型來進行預測。我們想要建立的就是表達數值與值的關係模型。

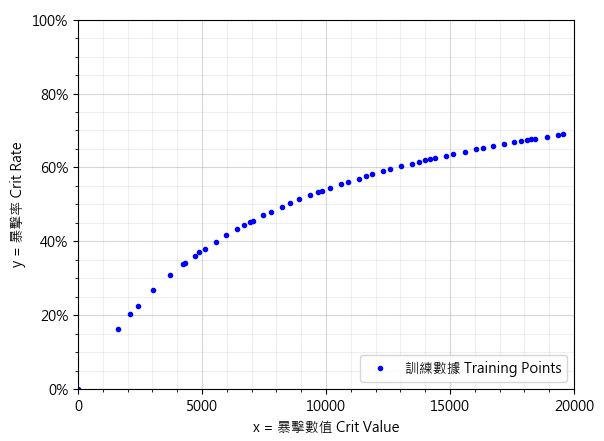
「圖3」暴擊（60等）數據點畫在坐標系上

由於數據點連起來的很明顯是非線性(Nonlinear)的，我們先嘗試以多項式迴歸(Polynomial regression)來進行分析，即使用x的多次方程式來表達y。我們可以使用scikit-learn的sklearn.preprocessing.PolynomialFeatures來建構模型。建構的過程就跳過（有興趣的朋友可以在下文的GitHub連結找到原始碼檔案），直接把多項式展示出來吧。

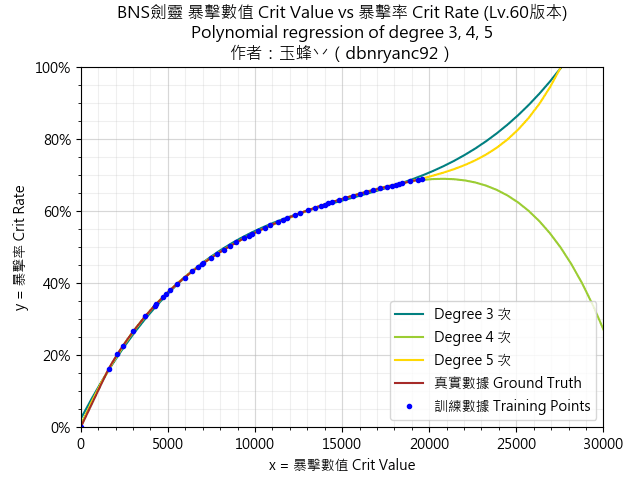
「圖4」暴擊（60等）數據進行多項式迴歸後建構的3, 4, 5次方程式

很明顯地可以看出來，x在有提供數據的範圍內（即0-19564），無論是幾次的多項式都能夠很不錯地表達y，但是若要預測更高數值的x，由於超出了數據的範圍，準確度則大幅下降了。這樣並不符合我們的需求，因為沒辦法估算裝備提升後的效果。

為了讓算式有更佳的表達能力和預測能力，我們應該先找到一個適合的模型。最後我們選擇了米氏方程(Michaelis-Menten equation)作為預設模型(Preset model)。方程可以表達為：

「算式2」米氏方程(Michaelis-Menten equation)表達式

由於我們有一個預設的模型函數了，所以可以使用SciPy的scipy.optimize.curve_fit來尋找最佳擬合曲線(Best-fit curve)。curve_fit的原理是使用最小平方法(Least squares method)來最小化(minimize)預測數據與實際數據間的誤差。建構模型的過程就一樣跳過吧，重要的是curve_fit回傳給我們的系數，我們把拿到的系數代入表達式放進圖表裡看一下效果。

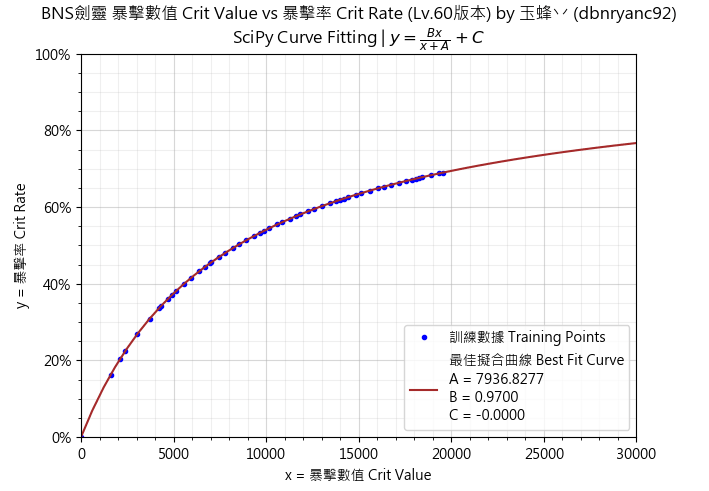
「圖5」暴擊（60等）數據及其最佳擬合曲線

這次的結果相當令人滿意。不但能準確地表達有提供數據的範圍，在預測的部份也相當優異。同樣的分析可套用在其他屬性上。

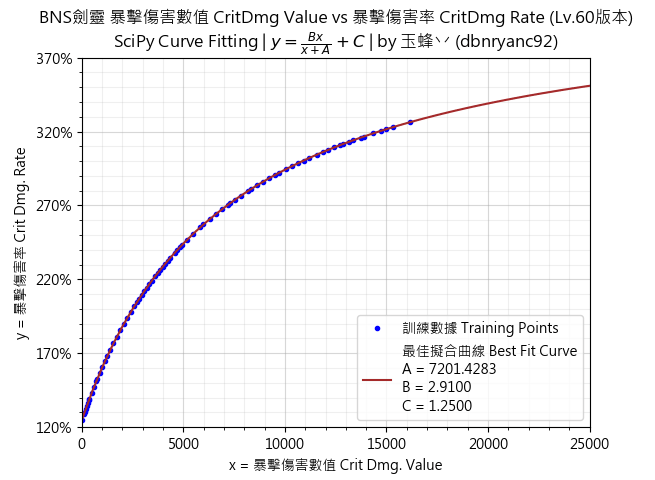
「圖6」暴擊傷害（60等）數據及其最佳擬合曲線

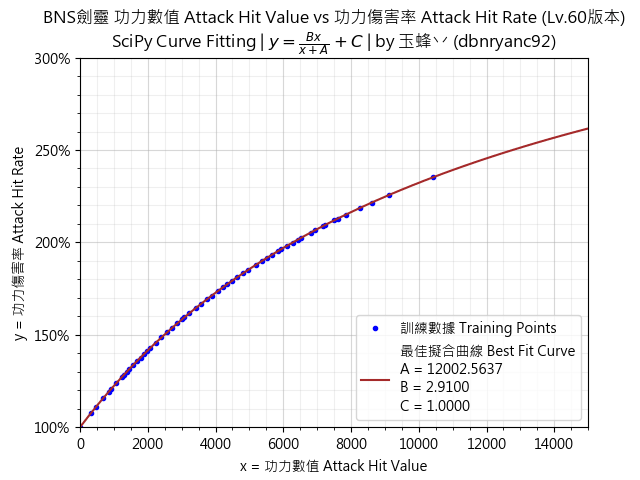
「圖7」功力（60等）數據及其最佳擬合曲線

「圖8」異常狀態傷害（60等）數據及其最佳擬合曲線

此部份所使用的資源，包括：

• 原始數據：csv格式
• 分析模型：py格式，Python腳本
• 輸出圖表：png格式

皆上傳到我的GitHub：dbnryanc92/ BNSAttributeCurveFit

---

屬性數值關係曲線及算式的特性

上一部份所示的分析結果，已經能很好地表達我們提供的原始數據了。但是由於從遊戲裡面的數據（主要是率的部份）並非準確(Exact)，而是四捨五入後的輸出(Rounded output)，所以curve_fit可能會把這些誤差也考慮到擬合的曲線裡面。為了更進一步提升準確度，那就只好手動調整各系數了。實際上由於curve_fit回傳的系數已經相當準確了，所以相當輕鬆地就把各屬性的關係曲線與原始數據的絕對誤差(Absolute error)壓在±0.005%的範圍內，亦四捨五入的誤差容限(Tolerance)。以下將展示系數調整後的算式。

「算式3」暴擊（60等）數值關係曲線算式

「算式4」暴擊傷害（60等）數值關係曲線算式

「算式5」功力（60等）數值關係曲線算式

「算式6」異常狀態傷害（60等）數值關係曲線算式

對原始數據的數值套用以上算式計算率後，得出以下關於誤差的統計。

屬性	平均誤差 avg(y*-y)	最大絕對誤差 max|y*-y|
暴擊（60等）	-0.00045%	0.00453%
暴擊傷害（60等）	-0.00037%	0.00499%
功力（60等）	0.00027%	0.00493%
異常狀態傷害（60等）	0.00065%	0.00486%

這些關係曲線的算式有幾個特點值得一提。讓我們再看一次我們的算式模型。

「算式2」米氏方程

1.    最小值為C

由於x代表屬性數值，所以函數的定義域(Domain)為大於等於0的正整數。由於這是一個漸增(Increasing)函數，所以當x為最小值時，y也是函數值域(Range)的最小值。當為0時，y=C。

同樣地，當x為最大值時，y也是函數值域的最大值，y=B+C。

「算式7」米氏方程在的最大值

把x=A代入方程，就會得出y = ((C)+(B+C))/2 = B/2+C

把以上幾個特性套用在暴傷的關係曲線上，我們就可以得知以下幾點：

• 當你暴傷數值是0的時候，暴傷率為125%
• 無論你暴傷數值再高，暴傷率不會超過416%
• 當暴傷數值為7201的時候，暴傷率為大約270.50%

需注意的是，上面提到的暴傷率為暴傷數值轉換而成的暴傷率，計算面板暴傷率還要考慮其他影響面板暴傷率的因素（如龍銀會員），而實戰時亦要加上其他增益(Buff)效果的暴傷率，該些效果的暴傷率亦不受上述最大值影響。

---

如何應用這些算式

應用一、快速轉換屬性數值和率

回歸到本文最一開始的目標——把裝備上部份白字的屬性（例如暴擊傷害、功力）轉換成傷害算式裡面的數值，現在是不是可以輕鬆完成呢？為了方便計算，我製作了一個簡易的屬性數值換算工具，只要輸入6格資料，你要的結果就顯示出來了。（建議「建立副本」再使用）

20200201更新：由於Google表格在設計編輯權限上有很多限制，導致表格被無意弄壞／有意破壞了好幾次，所以屬性數值換算工具已轉移到另一個本人製作的網頁上面啦。

「圖9」屬性數值換算工具使用範例一

先來示範一下如何把「數值」轉換成「率」。如果我現在暴傷數值為16098，我希望知道3層獨角大王燒酒（共600暴傷）對暴傷的提升有多少，我只要把6個灰格都填入我的數值/資料，下方就正確顯示現在的面板暴傷率400.06%，同時亦預測新的面板暴傷率為402.32%。也就是說當你暴傷數值為16098時，600暴傷數值只會讓暴傷率提升2.26%，對總傷害升幅只有0.56%（就是其實沒甚麼用）。不過不要忘記這只是面板屬性的升幅，實際上還有其他Buff、技能有提升屬性的效果，所以實戰時升幅更低（實際是多少就需要每個Buff逐一計算了）。

「圖10」屬性數值換算工具使用範例二

然後我們來看「率」轉換成「數值」的部份。如果我現在面版暴擊率為96.39%，我想知道需要多少額外暴擊數值，面板暴擊率才會到達100%。輸入所需資料後，就會發現只需要約4195點暴擊，就會達成目標。

應用二丶比較不同等級的屬性

不知道大家有沒有注意到，上文在描述屬性的時候都會補上「（60等）」的標籤。實際上這是非常關鍵而且不能省略掉的，因為在不同等級的時候，同樣的屬性數值對應的率是不一樣的。說起來好像很虛幻，但其實大部份玩家都知道的：每當新版本有提高等級上限的時候，你等級往上升，面版屬性率就往下掉了。例如在天舞宮（2019年6月）版本，等級上限從55提高到60，很多玩家就說暴擊率下降了5%。這其實就是因為在不同等級的時候，屬性關係曲線的系數是不一樣的。

剛好我手頭上有55等的暴擊原始數據（55等版本的時候就已經收集了，但是那時候沒有空進行研究，也沒有收集其他屬性的數據，有相關數據的朋友歡迎提供給我或者自行分析），所以我以同樣的方式去尋找系數。以下將顯示結果的相關數據和圖表：

「圖11」不同等級下的暴擊屬性最佳擬合曲線

「算式8」暴擊（55等）數值關係曲線算式

屬性	平均誤差 avg(y*-y)	最大絕對誤差 max.|y*-y|
暴擊（55等）	0.00065%	0.00568%

從兩條曲線就很明顯可以看到在同樣的數值下，率的確是變低了，但是變低多少卻不是固定的。在數值為6549的時候率下降最多，降低了9.3%，但當數值再往上時，率的下降就變少了。其原因跟數值變高時，增加的率會遞減有關。

然後我們可以對比一下55等跟60等的暴擊的曲線算式，這裡我們可以發現其實只有一個系數（Ａ）有改變，其他兩個都是不變的。既然算式那麼接近是不是有甚麼含意呢？簡單推演一下算式後，原來系數A的升幅就是同一個率所對應的數值的升幅。我們直接代入數值來說明，60等的算式中系數Ａ是55等系數A的約1.47倍，也就是說當我們從55等升到60等以後，需要本來暴擊數值的約1.47倍，暴擊率才會回復到等級提升前一樣（好坑喔）。

欸？既然55等和60等的算式我們都知道了，那我們是不是就可以預測未來版本（例如說65等）的算式呢？的確由於算式當中只有一個系數改變了，只要我們再把那系數改動一下，是有可能預測未來版本的數據的。但是！我現在手頭上只有兩個等級的算式，數據量有點有少，所以沒有辦法確定系數的變動是不是存在特定的關係（線性？指數？對數？），也有可能是韓國策劃按其他準則來定的。所以我們只能嘗試作出小預測，卻沒有辦法完全證明我們預測是否準確哦（除非有更多不同等級的數據A_A）。以下是以等比的方式調整系數後的結果圖：

「圖12」推測未來版本的暴擊屬性關係曲線

重申一次，上圖純屬推測，而非實際數據！不過說那麼多，未來是不是真的會65等，或者開放的時候我還有沒有在玩已經不好說了（有生之年系列！？）。所以這部份看看就好，不必認真。關於55等暴擊的數據和圖表也都上傳到GitHub：dbnryanc92/ BNSAttributeCurveFit

---

後記

說實話做這類研究其實有點自嗨，因為實際作用並不大。「玩個遊戲而已，那麼認真幹嘛」「就算知道了這些數據又能怎樣」……不過對我而言，這無疑是一個寓學習於遊戲的機會，就把學到的知識應用一下這樣。然後事實上，這次研究的主題對我自己和朋友們升裝備的選擇上也有一定幫助。本來有在猶豫這類型的研究是不是應該收起來給自己和有興趣的朋友參考就好，但是因為這個滿有趣的，更重要的是，我觀察到近期在討論劍靈的主流中文社群中，甚少有以數據為核心的分享，所以希望公開這篇能有拋磚引玉的作用。事實上，如果是熟悉我的朋友應該也知道我還有滿多其他關於劍靈的研究，有機會的話也會考慮公開分享看看（不過就要看這類型的分享有沒有關注度了）。

虎嘯龍吟的數學系玩家

玉蜂丷（丶小肥蜂）

---

20191103 補充

另外關於屬性在不同的數值下的效益，可以透過各屬性關係曲線算式的一階導數(First derivative)，去找出屬性的邊際效益（即在特定數值下額外增加1點的效益／曲線在特定一點的斜率）。

設f(x)為60等暴傷曲線算式；g(x)為60等功力曲線算式。兩者的一階導數算式如下：

「算式1」暴擊傷害（60等）的邊際效益

「算式2」功力（60等）的邊際效益

「圖3」60等暴擊傷害和功力的邊際效率比較

簡單來說只要你把某屬性的數值代入x，再找出x在該屬性曲線對應y的值，就是該屬性在特定數值下的效益了。