這篇就來說說關於三角函數中的「積化和差,和差化積」,為什麼要學這個?
雖然已經沒放在現今的高中課綱之中了,早在99年那次的教改中,就將此移除課綱外了。
當時的理由是:『高中數學科、物理不涉及不同週期之三角函數的疊合,故無必要性,且易發展出太難的題型。』
其實蠻合理的,就實用性上來說,確實沒那個需求,反而最後變成考試會出無謂的題目造成學生更多負擔而已。
不過有些高中老師還是會補充,甚至放在段考或是小考折磨學生XD
相信有些高中生在高中的三角函數單元應該有看過,不過不用擔心,學測與指考是不會考的。
但是呢,已經被課綱拿掉的東西,難道就不重要嗎?希望大家可以想想看這個問題。
我們不應該是為了分數學習,而是為了求知、為了數學!
這邊就請大家放下已見,不要被無聊的題目束縛,從歷史的觀點、數學的發展來欣賞這樣的積化和差吧。
首先,我們先來推導一下這個公式,不要去死背它,了解公式的來由以及想法,這樣就算忘了,還是可以自己推導出來,最早在16世紀,應該是由一位叫做維埃塔(弗朗索瓦·韋達,法語:François Viète 1540年-1603)的數學家於其著作《應用於三角形的數學法則》中提到。
那時正值大航海時代,對於航海定位與天體與大地測量有極高的需求,三角學也在此蓬勃發展!此數學家維埃塔對三角學貢獻良多,有興趣的人可以查查。
「三角函數乘積能否化簡為三角函數的和?」 我想這就是最一開始的想法,這邊提到的三角函數先都以sin和cos為主,畢竟其他的三角函數都可以用sin與cos作表示。
一般來說,做加法運算總是比做乘法運算還來的容易與簡單,更何況在當時那個年代,沒有計算機,要將兩個三角函數值相乘絕對是比相加麻煩許多的,當時僅有三角函數表,若能夠利用查表得出其值,做加減運算便可得出三角函數的乘積那就太好了
那我們就先來考慮三角函數的乘積: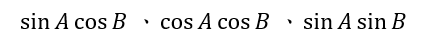
利用我們已知的三角函數知識,會出現兩個三角函數乘積的,應該會想到和差角公式:
不難看出來,想要將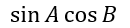 表示出,其實就是將
表示出,其實就是將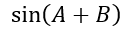 與
與 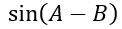 作相加再除2就好了,
作相加再除2就好了,
便得到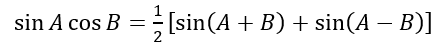
類似的手法,我們也得到:
這就是積化和差。(不過其實二式跟一式是一樣的)
積化和差推導出來了,現在來想想和差化積,就是反過來;將三角函數的加減化為三角函數的乘積
其實就是利用上面推導出來的公式逆推,不妨令X=A+B、Y=A-B 做代換,A=(X+Y)/2 、B=(X-Y)/2
便可有:
用類似的手法,一樣可以有:
(注意,最後一式會有負號,實際如何應用還是要看情況,不要死背。)
那麼,我們試著假設我們是當年的人,使用積化和差來計算看看吧
我們就來算sin(53°) * cos(28°)
如果不使用積化和差,查表得值後去算,會很累
就是0.7898 * 0.8829 ( 這邊都是以上面的三角函數表中的近似值做運算)
那我們使用積化和差公式,便可以這樣算:
sin(53°) * cos(28°) = (1/2) * ( sin (81°) + sin(25°))
= (1/2) * ( cos ( 9° ) + sin(25°)) = (1/2) * (0.9877 + 0.4226)
= (1/2) * (1.4103) = 0.70515
用wolfram alpha 來驗證看看
很接近了
若是其他大數,也可以用技巧做變換。這樣的做法在當年應該會比較有實用價值才對
例如:
想要算 20.22 * 122.4
為了使用積化和差,必須將數化成介於(0,1)之間的小數乘上10的次方來寫
得到20.22 * 122.4 = (0.2022 * 10^2 ) * (0.1224 * 10^3) = 0.2022 * 0.1224 * 10^5
那麼只要查表找出,sinA = 0.2022 、cosB = 0.1224 的兩角 A 和 B (當然你也可以找sinB=0.1224)
接著便是用我們的積化和差公式:把A、B代入
最後再乘上10^5 便可得到 20.22 * 122.4
(這邊就不繼續做啦,實際上是那個表沒有0.1224的直接對應角度,必須使用內插法來求,可見有更精確的表有多重要)
感覺很麻煩?是嗎?現在有計算機,當然覺得麻煩,但要知道當年的人,沒有計算機、沒有電腦、沒有手機,如果是很大或是很小數字做相乘除,用積化和差的做法是更實際的。以實用面來說,也不一定要求到精確值,有個近似值就夠用了,當然數字越多位,誤差就越大,使用更精確的三角函數表是個大課題。
題目欣賞:
試求 之值
之值
直接求是不可能的,所以當然要點技巧,正是這篇文說的積化和差,可以想想看喔,下面馬上就要解題了,不想被破梗的人可以想一下再下拉。
不妨先令其值為p,接著乘上 2sin(2π/7) 使其可以積化和差,最後再除回去便可求得其值p
其實算是積化和差的經典題型,有一系列這樣的題目。
其實呢,這是曾經我在某次考試中遇見的題目...當時我只會把課本上的公式學好,對於這樣的題目完全沒想法,而那次考試班上大家考得很差,考完後繼續趕課,老師也沒去檢討這樣的題目了,然而我自己去查,發現必須要用積差化和的做法。決定不要忘記這個積化和差了。
(個人是頗討厭,老師考出來都不檢討這種作為的啦,以為不會就算了,沒人要問是不是?沒關係的,我會自己找出答案,實際上那不過就是積差化和的技巧,然而當時已經刪除於課綱之中。老師更是沒提過,事後問老師感覺他本人也不太知道做法,考這題存心是不讓人拿分的。大概只是隨便從題庫抓一題看起來很難的題目來吧...
還很多題目,這邊的重點不是解題,就不放上了,有興趣的人自己找找,或是再交流都可。
最後,為何要學積化和差,這樣的公式?
在二十一世紀的現代,有計算機可以使用,想要求任意三角函數值相乘的話,使用電腦手機按一按就能把數值算出來了,還要學這個公式做什麼?時空背景早就不一樣了。
這樣說沒錯,時空背景已經不同了,二十一世紀的現代,已經不是過去還得查表手算的那個年代了。
但,還有一個重點,就是在積分上會用到,在大學的微積分中,在積分的單元時,三角函數的積分那邊,應該會碰到這樣的題目:
這時就必須使用積差化和,我們便可以很快地完成此積分了!
(C是常數,記得加)
把複雜的三角函數乘積化簡為簡單的三角函數和差,便可以輕鬆地做積分!
這就是積化和差的重要性!
在二十一世紀的現代,積化和差早就不是為了化簡複雜的運算、也非為了求那些被設計過的題目,是為了積分。
當然在許多三角函數的恆等式與式子的運算之中也會用到,可以推出許多美妙的公式,但那就稍微高深冷僻一點,一般人大概也少碰到,有機會在未來介紹。
之前翻一下以前小屋的文章才赫然發現人氣最高的居然是很久以前寫的數學文,說來好笑,現在來看都是有待加強跟缺乏數學素養的文章,覺得現在來寫應該可以有不一樣的表現吧,多少對得起以前那個充滿妄想的自己,也希望對社會大眾能有點幫助;想要數學更強的人、喜歡數學的人、學不好數學的人、對學校中的數學沒興趣的人、覺得數學沒用的人、覺得數學無聊的人... 都可看看。
有什麼意見都說,有誤的地方請大聲斥責。還請多多關照。
不定期發文,看心情與動力吧,有空的話希望能多打一點。
雖然我還是很弱小,但要慢慢往上爬,在這數學的荒野繼續探索。
應該也有像我這樣的小卒能做到的事情吧。